9rytna vous proposez un exemple d'examen de recherche opérationnelle (Ro° S5 option économie avec corrigé, l'examen il traiter des cas et des problèmes de recherche opérationnelle (RO), vous allez trouver ci-dessous l'examen avec une corrigé bien détaillé.
Examens de recherche opérationnelle (RO) S5
Examen(Enoncé) :
1) Répondre par vrai ou faux aux questions suivantes : Soit A ∈ Mm,n, x ∈ Rn, b ∈ Rm
a) Ax = b forme standard simpliciale ⇒ m ≤ n A= [Im/H] H M(R)
b) Ax = b forme standard ⇒ Ãx ≤ b forme canonique Ã∈ M(R) b∈ R²
c) 2x1 + x2 ≤ 5, 2x2 + x1 ≤ 5 deux contraintes redondantes
d) Un ensemble E ⊂ R est convexe si x1, x2 ∈ E, ∀λ∈R⇒ λx1 +(1- λ)x2 ⇒ x1 = x2 = X̅
e) est point extrémal de E, il existe x1, x2 ∈ E et λ∈ [1;2] telle que X̅ = x1 = x2
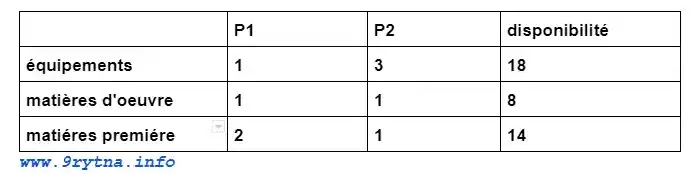
Une usine fabrique de produits P1 et P2 nécessitant des ressources d'équipement de, de main d'ouvre et de matière premières disponibles en quantité limitée.
P1 et P2 rapportent à la vente de 30 DH et 20 DH par unité.
1) Quelle quantité de produit P1 et P2 doit produire l'usine pour maximiser le bénéfice total venant de la vente des deux produits ?
2) Supposons que la vente de P2 augmente de 10DH, chercher la valeur maximale de Z.
3) Donner l'interprétation économique de la solution optimale.
Exercice 2 :
On considère PL suivante :
Résoudre PL à l'aide de la méthode du simplexe : par méthode révisée et méthode des tableaux.
1) Ecrire les problèmes duals (D1) de (P1) et (D2) de (P2).
2) Appliquer sur (P2), le théorème des écarts complémentaires pour vérifier l'optimal de la solution proposée X̅ = (3,2,0,0,1)
Examen (Corrigé)
1) a) Vrai ( définition de la forme simpliciale)
b) Vrai ( le passe de canonique)
c) Faux (à vérifier)
d) Vrai (définition d'un convexe)
e) Vrai (définition d'un point externe)
2) voir le support de cours
On a z = 30x1 + 20x2 = P ⇒ Max z = Max 30x1 + 20x2 = Max P
30x1 + 20x2 = B ⇒ 20x2 = -30x1 + P ⇒ x2 = -30x1/20 + p/10 =-3x1/2 +p/20
le coefficient est (1,-3/2)
(D1) : x1 + 3x2 = 18
pour x1 = 0 ⇒ x2 = 6
et x1 = 18 ⇒ x2 = 0
(D2) : x1 + x2 = 8
pour x1 = 0 ⇒ x2 = 8
et x1 = 0 ⇒ x2 = 8
(D3) : 2x1 + x2 = 14
pour x1 = 7 ⇒ x2 = 0
et x1 = 0 ⇒ x2 = 14
x1 + x2 = 8 et 2x1 + x2 = 14 ⇒ Δ = 1-2 = -1 ≠ 0
Δx1 = 8 - 14 = -6
Δx2 = 14 - 16 = -2
x1= Δx1 / Δ = -6 / -1 = 6
x2 = Δx2 / Δ = -2/-1 = 2
on a x1 = 6 et x2 = 2 ⇒ z* = 30*6 + 20*2 = 180 +40
z* = 220
2) Le prix de P2 augmente de 10 DH alors la fonction objectif sera changé ⇒ la nouvelle fonction sera : Max 30x1 + 30x2
On a P(Z) = -30/30 =-1
P(D1) = -1/3
P(D2) = -1
P(D3) = -2
On a P(Z) = P(D2) = -1 ⇒ (Z) (D2)
Puisque (D2) donne le plus point dans la figure alors la solution optimal sera les points de la région réalisable qui appartient à la droite (D2) ⇒ la solution est le segment [BC]
Donc Z* = 30*6 + 30*2 + 180 + 60
Z* = 240
3) Si le prix est augmenté de 10DH alors la marge bénéficiaire sera 240. cette marge peut être réalisé par plusieurs méthodes de production : 6 unités de P1 et 2 Unités de P2 (Sommet B).
5 unités de P1 et 3 unités de P2 (sommet C)
4 unités de P1 et 4 unités de P2 (milieu de [BC])
2x2 - x3 = 1 ⇔ - x3 = 1 - 2x2 ⇔ x3 = -1 + 2x2 < 0 ⇒ non réalisable
alors on change la base
Donc on aura : 2x2 - x3 = 1 ⇔ 2x2 = 1 + x3 ⇔ x2 = 1/2 + x3/2
Max 2x2 = Max 2(1/2 + x3/2) = Max 1 + x3
x1 + x2 + x4 = 2 ⇔ x1 + 1/2 + x3/2 + x4 = 2
⇔ x1 + x3/2 + x4 = 2 - 1/2 = 3/2
Max 1 + 3
x2 - x3/2 = 1/2
x1 + x2/2 + x4 = 3/2
Nb : ce changement de base est facultatif je peux bien résoudre sans le faire, la base (x1,x4) mais avec une résolution par méthode dictionnaire.
On a la fonction objective est Max 2x2
Alors Max z = Max 2x2 ⇒ Max x2 ⇒ x2>0
Donc les bases ne contient pas x2 sont des bases non optimale.
B1 = {x1,x2} ⇒ AB1 = (0 2 ; 1 1) detAB1 = -2 ≠ 0 ⇒ B1 base
1/AB1 = 1/-2(0 -2 ; -1 0) = (-1/2 1; 1/2 0) ⇒ xB1 = b/AB1
= (-1/2 1 ; 1/2 0)(1 2)
= (3/2 1/2) >0 ⇒ S.R.N.D
ĈMB1 = CMB1 - CB1.AB1/AB1
= (0,0) - (0,2) (-1/2 1 ; 1/2 0)(-1 0 ; 0 1)
= (0,0) -(0,2) (-1/2 1 ; 1/2 0)
= (0,0) - (-1,0) = (1,0)
donc non optimale.
B2 = {x2,x3} ⇒ AB2 = (2 -1 ; 1 0) detAB2 = 0 -(-1) = 1 ≠ 0 ⇒ B2 base
1/AB2 = (0 1;-1 2)
xB2 = ( 0 1;-1 2(1 2) = (2 3) >0 ⇒ S.R.N.D
ĈMB1 = CMB2 - CB2.AB2/AB2
= (0,0) - (2,0) (0 1 ; -1 2)(-0 0 ; 1 1)
= (0,0) -(2,0) (1 1 ; 2 2)
= (0,0) - (2,2) = (-2,-2) < 0 ⇒ solution optimale
x*(0,2,3,0) Z*= CB2xB2 = (2,0)(2 3) = 4
B3 = {x2,x4} ⇒ AB3 = (2 0 ; 1 1) detAB3 = 2 ≠ 0 ⇒ B3 base
1/AB3 = 1/2(1 0;-1 2) = (1/2 0; -1/2 1)
xB3 = (1/2 0; -1/2 1)(1 ; 2) = (1/2 3/2) >0 ⇒ S.R.N.D
ĈMB3 = (0,0) - (2,0) (1/2 0 ; -1/2 1)(0 -1 ; 1 0)
= (0,0) -(2,0) (0 -1/2 ; 1 1/2)
= (0,0) - (0,-1) = (0,1) < 0 ⇒ solution non optimale
Donc X* = (0,2,3,0), Z* = 4, Sommet ( 0,2)
On a : X̅(3,2,0,0,1)
2x1 + x3 + x2 - 8 = 2*3 + 0 + 2 8 = 0 ⇒ saturée ⇒ rien à conclure
2x2 + x1 + x4 - 7 = 2*2 + 3 +0 -7 = 0 ⇒ saturée ⇒ rien à conclure
x2 + x5 - 3 = 2 + 1 -3 = 0 ⇒ saturée ⇒ rien à conclure
On a :
X̅1 = 3 ≠ 0 ⇒ contrainte 1 saturée ⇒ 2y1 + y2 - 4 = 0
X̅2 = 2 ≠ 0 ⇒ y1 + 2y2 + y3 - 5 = 0
X̅3 = 0 ⇒ rien à conclure
X̅4 = 0 ⇒ rien à conclure
X̅5 = 1 ≠ 0 ⇒ y3 + 2y2 - 0 = 0 ⇒ y3 = 0
Donc :
y1 + 2y2 + y3 - 5 = 0 et 2y1 + y2 - 4 = 0 et y3 = 0 ⇒ y1 + 2y2 - 5 = 0 et 2y1 + y2 - 4 = 0
⇒ y1 = 5 - 2y2 et 10- 4y1 + y2= 0
⇒ y1 = 5 - 2y2 et y2= 2
⇒ y1 = 1 et y2= 2
⇒ Ӯ =(1,2,0) S.R du Dual.
On a :
Z = 4*3 +5*3
= 12 +10
Z = 22
W = 8*1 + 7*2
= 8 + 14
W = 22
Donc :
X̅(3,2,0,0,1) S.Op du (P2)
Ӯ =(1,2,0) S.Op du (D2)
Z*= W* = 22
Examens de semestre 5 option économie
1. Examens de histoire de la pensé économique
2. Examens de relations économiques internationales (REI)
3. Examens d'économétrie 1
4. Examens de comptabilité nationale
5. Examens de finances publiques II
Support de recherche opérationnelle (RO) S5
- Cours de recherche opérationnelle (RO) S5
- Résumé recherche opérationnelle (RO) S5
- Exercices recherche opérationnelle (RO) S5


Enregistrer un commentaire