Le résumé de statistique descriptive vise à donner pour les étudiants de semestre 1 filière économie et gestion les informations les plus importantes concernant le module de statistique descriptive pour but de faciliter la préparation afin de maîtriser les axes les d'informations aux matières de statistique descriptive S1.
Statistique descriptive S1 - Licence 1 Semestre 1 : Résumé
La statistique descriptive est un module pratique étudié au semestre 1 vise à donner les bases, relations et les méthodes utilisées pour résoudre des problèmes économiques, le résumé contient plus d'informations concernant les axes vues au cours de statistique descriptive, à quoi sert le résumé de statistique descriptive ? Quels sont les axes les plus importants dans le cours de statistique descriptive S1? Quel est le but de résumé de statistique descriptive S1 ?
Pour voir plus de supports concernant le module de statistique descriptive vous allez les trouver ci-joints, pour les autres modules de semestre 1 vous allez trouver dans le site.
À quoi sert le résumé de statistique descriptive S1 ?
Le résumé de statistique descriptive S1 vise à collecter et résumer les informations les plus importants vues au cours afin de faciliter la préparation pour les étudiants.
Il y a des résumés qui peuvent annuler des informations qui sont très importantes pour des professeurs par rapport aux autres professeurs dans vous êtes obligés de savoir quels sont les axes que le professeur à insister de les maîtriser afin de ne pas perdre des informations qui vont procurer des obstacles au jour d'examen.
Quels sont les axes les plus importants dans le cours de statistique descriptive S1 ?
Personne ne peut dire que cet axe ou cette partie est plus importante que l'autre, tout les axes et les parties traités au résumé de statistique descriptive S1 ont une importance.
Quel est le but de statistique descriptive S1 ?
Comme on a mentionné précédemment, le but de résumé est de faciliter la préparation pour les étudiants.
Le support
Le support contient les informations qui traitent le résumé de statistique descriptive S1, si vous avez besoin à ses informations vous pouvez nous contacter sur la page nous contacter.
I) UN PEU DE VOCABULAIRE
Toute étude statistique s'appuie sur des données. Dans le cas ou ces données sont numériques (99% des cas), on distingue les données discrètes (qui prennent un nombre fini de valeurs : par ex, le nombre de voitures par famille en France) des données continues (qui prennent des valeurs quelconques : par ex, la taille des animaux d'un zoo).
• Dans le cas d'une série discrète, le nombre de fois ou l'on retrouve la même valeur s'appelle l'effectif de cette valeur. Si cet effectif est exprimé en pourcentage, on parle alors de fréquence de cette valeur. (cf 17 p82)
• Dans le cas d'une série continue, on répartit souvent les données par classes. (cf 13 p82) Dans les exercices, les données se présenteront donc ainsi :

Le but des statistiques est d'analyser les données dont on dispose :
-
Pour cela, on peut s'aider d'un graphique : Nous verrons notamment cette année les diagrammes à bâtons, les
histogrammes et les diagrammes en boîtes (ou à moustaches).
-
On peut aussi chercher à déterminer la moyenne ou la médiane de la série. De tels nombres permettent
notamment de comparer plusieurs séries entre elles. On les appelle indicateurs statistiques ou paramètres statistiques. On distingue les indicateurs de position (qui proposent une valeur "centrale" de la série) et les indicateurs de dispersion (qui indiquent si la série est très regroupée autour de son "centre" ou non).
Nous étudierons cette année les indicateurs statistiques suivants :

II) DIAGRAMMES A BATONS OU HISTOGRAMMES
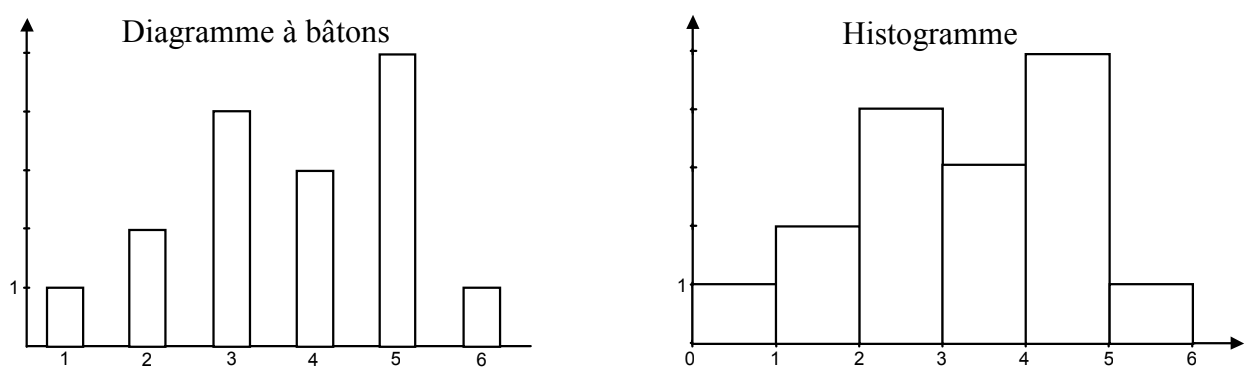
1) Quelles différences voyez-vous entre les deux graphiques ci-dessous ?
-
Dans le diagramme à bâtons, l'axe des abscisses n'est pas gradué et la largeur des bâtons ne signifie rien.
-
Dans l'histogramme, l'axe des abscisses est gradué et les bâtons sont donc "collés" les uns aux autres.
L'histogramme est donc surtout utilisé pour représenter graphiquement des séries continues où les données ont
été réparties en classes.
-
Attention, Excel appelle histogramme les diagrammes à bâtons et ne sais pas faire de vrais histogrammes !
2) Le cas des classes d'amplitudes différentes
Pour représenter la série ci-contre, quel est le graphique le plus équitable ?

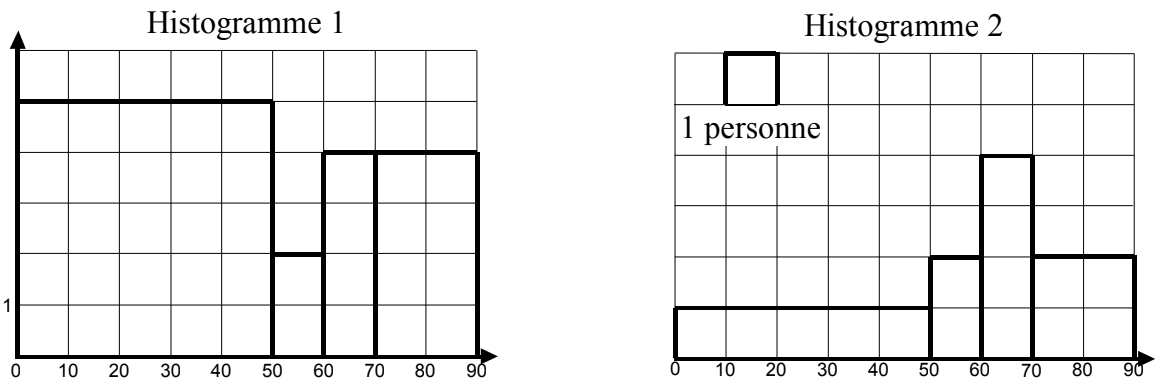
• L'histogramme 1 est inadapté car il laisse entendre que la majorité des gens pèsent moins de 50 kg !
• L'histogramme 2 est équitable car on a pondéré la hauteur de chaque bâton en tenant compte de l'amplitude de
la classe. Pour construire ce deuxième histogramme, on réalise le tableau ci-dessous :

Remarques :
-
Dans l'histogramme 1, c'est la hauteur des bâtons qui permet de lire l'effectif. Dans l'histogramme 2, c'est l'aire des bâtons qui permet de lire l'effectif.
-
Dans l'histogramme 2, nous n'avons pas tracé l'axe des ordonnées, car il aurait fallu le graduer en nombre de personnes par kilo ! Par contre, pour permettre la lecture du graphique, nous avons indiqué en légende la signification de l'unité d'aire.
-
Dans les exercices, quand les classes ont toutes la même amplitude, on fait un histogramme de type 1, quand les classes ont des amplitudes différentes, ont fait un histogramme de type 2.
III) MODE, ETENDUE
1) Définitions
Si les données d'une série sont discrètes, le mode est la ou les valeurs qui ont le plus grand effectif. Si les données ont été réparties en classes, on parle alors plutôt de classe modale.
L'étendue d'une série est la différence entre la plus grande valeur et la plus petite.
2) Dans les exercices :
a) Données discrètes 9, 11, 8, 10, 13, 12, 10, 11, 10
Faisons le tableau des effectifs :
• Le mode est la valeur qui a le plus gros effectif, c'est à dire
• 13 - 8 = 5
Remarque :
Ici, vu le petit nombre de données, faire un tableau des effectifs est un peu artificiel. Par contre, dès que l'on travaille sur un nombre important de données, il devient vite très utile pour mettre en évidence le mode et l'étendue de la série.
b) Données réparties par classes
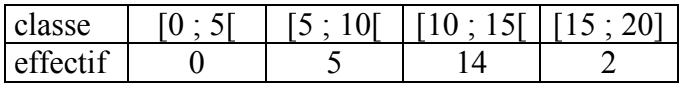
• La classe modale est la classe qui a le plus gros effectif, c'est à dire la classe • 20 – 5 = 15 donc l'étendue de cette série est inférieure ou égale à
Remarque :
Par simplification, on dira souvent que l'étendue est 15 mais c'est un abus de langage ! En effet, dans le tableau des données ci dessus, rien ne permet d'affirmer que les valeurs extrêmes sont 5 et 20 !
IV) MEDIANE, QUARTILES, DECILES
1) Définitions
Soit une série rangée par ordre croissant. Appelons n l'effectif total de la série. Définitions Pour déterminer le rang
|
La médiane • C'est la valeur "centrale" de la série. On dit qu'elle partage la série en deux moitiés |
|
|
Les quartiles (partagent la série en 4 : il y en a donc ) • Le 1er quartile Q1 est la plus petite valeur telle que 25% des données lui soit inférieures ou égales. • Le 3ème quartile Q3 est la plus petite valeur telle que 75% des données lui soit inférieures ou égales. |
• Q1 est la valeur dont le rang est le premier entier supérieur ou égal à • Q3 est la valeur dont le rang est le premier entier supérieur ou égal à |
|
Les déciles (partagent la série en 10 : il y en a donc ) • Le 1er décile D1 est la plus petite valeur telle que 10% des données lui soit inférieures ou égales. • Le 9ème décile D9 est la plus petite valeur telle que 90% des données lui soit inférieures ou égales. |
• D1 est la valeur dont le rang est le premier entier supérieur ou égal à • D9 est la valeur dont le rang est le premier entier supérieur ou égal à |
Remarques :
• Les trois nombres Q1, méd, Q3 partagent la série en 4 parts égales (à une unité près)
•Q2 = D
• Si les données ont été réparties en classes, on ne peut déterminer la médiane exacte. En revanche, on appellera classe médiane, la classe qui la contient (et permet donc d'en donner un encadrement).
• L'intervalle [Q1 ; Q3] s'appelle l'intervalle interquartile.
• Le nombre Q3 – Q1 s'appelle l'écart interquartile.
3) Diagrammes en boîtes
Le diagramme en boîte d'une série à l'allure suivante :
Remarques :
-
Lorsque la série est trop importante, que l'on ne connaît pas les valeurs extrêmes ou qu'on les considère comme non significatives, on raccourci souvent les moustaches au déciles D1 et D9.
-
La boîte centrale représente l'intervalle interquartile et contient donc la moitié des données.
-
Vous devez légender votre diagramme (min, max, nom de la série) et graduer l'axe.
-
On emploie surtout ce type de diagramme pour comparer plusieurs séries entre elles.
-
Ces diagrammes ont reçu beaucoup de noms différents : boîtes à pattes, diagrammes à moustaches,...
Ex :
Deux classes de 1L comparent leurs résultats du trimestre et déclarent : "nos classes ont le même profil puisque dans les deux cas la médiane des résultats est 10". Qu'en pensez-vous ?
V) MOYENNE, ECART TYPE, DONNEES GAUSSIENNES
1) Définitions

Remarques :
-
L'écart type mesure la dispersion de la série autour de sa moyenne.
-
Vous entendrez aussi parler de variance de la série. Il s'agit en fait de σ2
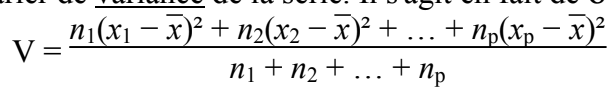
L'avantage de l'écart type sur la variance est qu'il s'exprime, comme la moyenne, dans la même unité que les
données.
• Dans le cas de données regroupées en classes, on ne peut calculer la valeur exacte de la moyenne ou de l'écart
type. On peut toutefois en déterminer une bonne approximation en remplaçant chaque classe par son milieu dans les formules ci-dessus.
3) Propriétés
a) Addition ou Multiplication de toutes les données par un même nombre :
Ex Soit la série : 10, 12, 14.
Ajoutons 2 : la nouvelle série est : 12, 14, 16. Divisons par 2 : la nouvelle série est : 6, 7, 8.
Cas général :
Soit α un réel quelconque :
• Si l'on ajoute α à toutes les données,
• Si on multiplie toutes les données par α,
b) Moyennes partielles
Ex : Sur les 5 premières interros, Paul a eu 12,5 de moyenne. Il vient d'avoir 15,5 à la 6 Les notes ayant toutes le même coefficient, quelle est sa nouvelle moyenne ?
La somme des notes des 5 premières interros est : 12,5 × 5
La somme des notes des 6 interros est donc : (12,5 × 5 + 15,5)
La nouvelle moyenne est donc : ̄x = (12,5 × 5 + 15,5)/ 6 = 13
la moyenne augmente d'α l'écart type ne change pas
la moyenne est multipliée par α l'écart type est multipliée par α
Cas général : Si on réunis deux groupes disjoints ayant respectivement pour moyennes et effectifs, ̄x1 et n1 d'une part, ̄x2 et n2 d'autre part, la moyenne de l'ensemble sera alors :
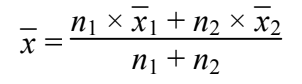
4) Moyenne et médiane
-
Quand on modifie les valeurs extrêmes d'une série, la moyenne change contrairement à la médiane qui ne change pas. On dit que la moyenne est "sensible aux valeurs extrêmes".
Il arrive que certaines de ces valeurs extrêmes soient douteuses ou influent de façon exagérée sur la moyenne. On peut alors, soit calculer une moyenne élaguée (c'est à dire recalculer la moyenne sans ces valeurs gênantes), soit utiliser la médiane. -
Comment interpréter un écart entre la moyenne et la médiane ? Soit la série suivante : 8 9 10 11 12
Ici la moyenne et la médiane sont identiques : la série est bien "centrée". Soit la nouvelle série : 8 9 10 12 14
Ici la moyenne est plus importante que la médiane : la série est plus "étalée vers la droite".
5) Données Gaussiennes
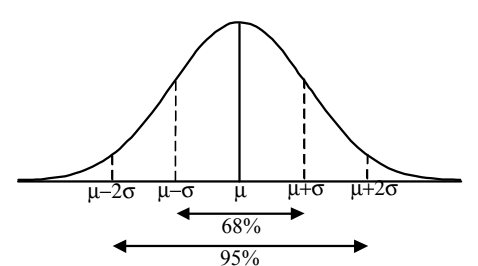
Dans de très nombreuses situations (issues de la biologie, géographie, sociologie, économie...) les données se présentent graphiquement sous la forme de courbes "en cloche" dites de Gauss.
Le comportement de ces séries est modélisable par une loi mathématique appelé loi normale ou loi de Gauss qui donne une grande importance à la moyenne μ et à l'écart type σ :
• Ces séries sont à peu près symétriques autour de μ
• Environ 68% des données sont dans l'intervalle [μ σ ; μ + σ]
• Environ 95% des données sont dans l'intervalle [μ σ ; μ + 2 σ]
• Environ 99% des données sont dans l'intervalle [μ 3 σ ; μ + 3 σ]
Les intervalles ci-dessus sont appelés plages de normalité pour les niveaux de confiance 0,68 ; 0,95 ; 0,99
Remarque : les observations ci-dessus n'ont aucun sens pour : Les séries qui traduisent des phénomènes non gaussiens
Les séries gaussiennes pour lesquelles l'échantillon est trop petit.
VI) QUELS INDICATEURS STATISTIQUES UTILISER ?
Dans la pratique :
-
On utilise très peu le mode et l'étendue (faciles à déterminer mais simplistes !)
-
On utilise la médiane, quartiles, déciles et écart interquartile surtout pour les séries à grands effectifs
(pas de calculs, il suffit d'ordonner la série ; peu sensible aux valeurs douteuses)
-
On utilise souvent la moyenne et l'écart type pour des séries de tailles intermédiaires ou des séries gaussiennes
(la moyenne reste l'indicateur leplus intuitif ; intérêt des plages de normalité)
Supports de module statistiques descriptives S1
Pour voir les autres articles concernant le module de statistique descriptive il suffit de cliquer ci-dessus sur le nom de l'article qui vous intéresse, si vous avez trouvé des manques des supports ou des informations vous pouvez le mentionner dans commentaire un ou nous contacter.


Enregistrer un commentaire